摘要:将南昌师范学院作为2021年江西专升本目标院校的小伙伴注意了,目前,2021南昌师范学院专升本高等数学专业考试大纲已经公布,相关专业的考生可根据考纲的要求及考试内容,找到正确的备考思路,从而更好地应对即将到来的2021年江西专升本考试。
将南昌师范学院作为2021年江西专升本目标院校的小伙伴注意了,目前,2021南昌师范学院专升本高等数学专业考试大纲已经公布,相关专业的考生可根据考纲的要求及考试内容,找到正确的备考思路,从而更好地应对即将到来的2021年江西专升本考试。

一、课程类别
理工科专业专升本课程
二、编写说明
1.本考核大纲参考同济大学数学系的教材《高等数学》进行编写。
2.本大纲适用于理工科专业专升本考试。
三、课程考核的要求与知识点
第一章函数、极限与连续
(一)函数
1.考核知识点
(1)函数的概念:函数的定义、函数的表示法、分段函数
(2)函数的简单性质:单调性、奇偶性、有界性、周期性
(3)函数的四则运算与复合运算
(4)基本初等函数:幂函数、指数函数、对数函数、三角函数、反三角函数
(5)初等函数
2.考核要求
(1)理解函数的概念,会求函数的定义域、表达式及函数值;
(2)理解和掌握函数的单调性、奇偶性、有界性和周期性,会判断所给函数的类别。
(3)理解和掌握函数的四则运算与复合运算,熟练掌握复合函数的复合过程。
(4)掌握基本初等函数的简单性质及其图象。
(5)了解初等函数的概念。
(二)极限
1.考核知识点
(1)数列极限的概念:数列极限的定义
(2)数列极限的性质:有界性、四则运算定理、夹逼定理
(3)函数极限的概念:x趋于无穷时
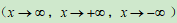
函数的极限,函数在一点处极限的定义、左、右极限及其与极限的关系
(4)函数极限的定理:夹逼定理、四则运算法则
(5)无穷小量和无穷大量:无穷小量与无穷大量的定义、无穷小量与无穷大量的关系、无穷小量的性质、两个无穷小量阶的比较
(6)两个重要极限
2.考核要求
(1)理解极限的概念(对定义中
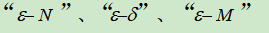
的描述不作要求),能根据极限概念分析函数的变化趋势。会求函数在一点处的左极限与右极限,了解函数在一点处极限存在的充分必要条件。
(2)掌握极限的四则运算法则。
(3)理解无穷小量、无穷大量的概念,掌握无穷小量的质、无穷小量与无穷大量的关系。会进行无穷小量阶的比较(高阶、低阶、同阶和等阶)。会运用等价无穷小量代换求极限。
(4)熟练掌握用两个重要极限求极限的方法。
(三)连续
1.考核知识点
(1)函数连续的概念:函数在一点连续的定义、左连续和右连续、函数在一点连续的充分必要条件、函数的间断点及其分类
(2)函数在一点处连续的性质:连续函数的四则运算、复合函数的连续性
(3)闭区间上连续函数的性质:有界性定理、最大值和最小值定理、介值定理(含零点定理)
(4)初等函数的连续性
2.考核要求
(1)理解函数在一点连续与间断的概念,掌握判断简单函数(含分段函数)在一点的连续性,理解函数在一点连续与极限存在的关系。
(2)会求函数的间断点及确定其类型。
(3)掌握在闭区间上连续函数的性质,会运用介值定理证明一些简单命题。
(4)理解初等函数在其定义区间上连续,并会利用连续性求极限。
第二章导数与微分
1.考核知识点
(1)导数概念:导数的定义、左导数与右导数、导数的几何意义、可导与连续的关系
(2)求导法则与导数的基本公式:导数的四则运算、导数的基本公式
(3)求导方法:复合函数的求导法、隐函数的求导法、由参数方程确定的函数的求导法
(4)高阶导数的概念:高阶导数的定义、高阶导数的计算
(5)微分:微分的定义、微分与导数的关系、微分法则
2.考核要求
(1)了解可导性与连续性的关系,会用定义求函数在一点处的导数。
(2)会求曲线上一点处的切线方程与法线方程。
(3)熟练掌握导数的基本公式、四则运算法则以及复合函数的求导方法。
(4)掌握隐函数的求导法、对数求导法以及由参数方程所确定的函数的求导方法
(5)理解高阶导数的概念,会求简单函数的高阶导数。
(6)理解函数的微分概念,了解可微与可导的关系,会求函数的一阶微分。
第三章中值定理与导数的应用
1.考核知识点
(1)中值定理:罗尔(Rolle)定理、拉格朗日(Lagrange)定理
(2)洛必达(L’Hospital)法则
(3)函数增减性的判定法
(4)函数极值与极值点最大值与最小值
(5)曲线的凹凸性、拐点
2.考核要求
(1)理解微分中值定理——罗尔定理、拉格朗日定理并会简单推证中值问题
(2)熟练掌握洛必达法则求
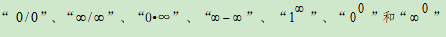
型未定式的极限方法。
(3)掌握利用导数判定函数的单调性及求函数的单调增、减区间的方法,会利用函数的增减性证明简单的不等式。
(4)理解函数极值的概念,掌握求函数的极值和最大(小)值的方法,并且会解简单的应用问题。
(5)会判定曲线的凹凸性,会求曲线的拐点。
第四章不定积分
1.考核知识点
(1)不定积分的概念:原函数与不定积分的定义、原函数存在定理、不定积分的性质
(2)基本积分公式
(3)换元积分法:第一换元法(凑微分法)、第二换元法
(4)分部积分法
2.考核要求
(1)理解原函数与不定积分概念及其关系,掌握不定积分性质,了解原函数存在定理。
(2)熟练掌握不定积分的基本公式。
(3)熟练掌握不定积分第一换元法,掌握第二换元法(限于三角代换与简单的根式代换)。
(4)熟练掌握不定积分的分部积分法。
第五章定积分
1.考核知识点
(1)定积分的概念:定积分的定义及其几何意义
(2)定积分的性质
(3)定积分的计算:变上限的定积分、牛顿一莱布尼茨
(Newton-Leibniz)公式、换元积分法、分部积分法
(4)定积分的应用:平面图形的面积、体积
2.考核要求
(1)理解定积分的概念与几何意义。
(2)掌握定积分的基本性质。
(3)理解变上限的定积分是变上限的函数,掌握对变上限定积分求导数的方法。
(4)掌握牛顿—莱布尼茨公式。
(5)掌握定积分的换元积分法与分部积分法。
(6)掌握直角坐标系下用定积分计算平面图形的面积
(7)掌握旋转体的体积计算
四、课程考核实施要求
1.考核方式
本考核大纲为理工科专业专升本学生所用,考核方式为闭卷考试。
2.考试命题
(1)试卷总分:150分
(2)考试时间:120分钟
(3)试卷内容比例:
函数、极限和连续约30%
一元函数微分学约35%
一元函数积分学约35%
(4)试题难易比例
容易题约40%
中等难度题约50%
较难题约10%
(5)题型有:选择题、填空题、讨论题、证明题、计算题
3.课程考核成绩评定
考试卷面成绩即为本课程成绩。
五、教材和参考书
1.教材
《高等数学》,高等教育出版社,同济大学数学系编
2.参考书目
[1]《高等数学》,邹杨、张艳霞等,四川大学出版社[2]《高等数学》,金宗谱等,吉林大学出版社

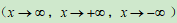 函数的极限,函数在一点处极限的定义、左、右极限及其与极限的关系
函数的极限,函数在一点处极限的定义、左、右极限及其与极限的关系
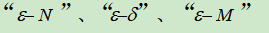 的描述不作要求),能根据极限概念分析函数的变化趋势。会求函数在一点处的左极限与右极限,了解函数在一点处极限存在的充分必要条件。
的描述不作要求),能根据极限概念分析函数的变化趋势。会求函数在一点处的左极限与右极限,了解函数在一点处极限存在的充分必要条件。
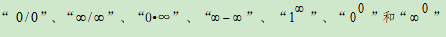 型未定式的极限方法。
型未定式的极限方法。





.png)