摘要:为方便准备报考2023年四川专升本的考生复习备考,现官方已经将2023年四川专升本高等数学考试大纲(文史类、财经类、管理类、医学类)公布了(文章底部附件可以下载),下面就和小易一起来看看后年高数将会考试什么吧!
为方便准备报考2023年四川专升本的考生复习备考,现官方已经将2023年四川专升本高等数学考试大纲(文史类、财经类、管理类、医学类)公布了(文章底部附件可以下载),下面就和小易一起来看看后年高数将会考试什么吧!

一、 总要求
考生应该理解或了解《高等数学》中函数、极限、连续、一元函 数微分学、一元函数积分学、多元函数微积分学、无穷级数、微分方 程和《线性代数》中的行列式、矩阵、向量的线性相关性、方程组的基本概念与基本理论。本课程的内容按基本要求的高低用不同的词汇 加以区分。对概念、理论从高到低用“理解”、“了解”、“知道”三级 区分; 对运算、方法从高到低用“熟练掌握”、“掌握”、“会”或“能” 三级区分。
考试用时: 120 分钟
二、 考试范围及要求
1、函数、极限与连续
( 1)理解函数概念(包括分段函数、复合函数、隐函数和初等函 数)和函数的两个要素;
(2) 掌握函数符号的意义, 会求函数的定义域和表达式及函数值 (包括分段函数);
( 3) 掌握基本初等函数及其简单性质、图象, 熟练掌握复合函数 的复合过程;
( 4)熟练掌握几个常用的简单经济函数(成本函数、平均成本函数、收益函数、利润函数、需求函数) 的经济意义、表现形式与相互关系;
( 5)会建立简单的实际问题的函数关系式(包括几个简单的经济函数);
( 6)了解函数与其反函数之间的关系(定义域、值域、 图象之间的关系及简单应用),会求单调函数的反函数。
( 7)了解极限的概念(对极限定义中的“ ε — N ”,“ ε —δ ”等 形式的描述不作要求)
( 8)会求函数在一点处的左右极限, 了解函数在一点处极限存在 的充分必要条件;
(9) 了解极限的有关性质, 掌握极限的四则运算法则;
( 10)理解无穷大量、无穷小量的概念, 掌握无穷小量的性质及其与无穷大量的关系,会进行无穷小量阶的比较;
( 11 )熟练掌握用两个重要极限求极限的方法;
( 12 )理解函数在一点连续与间断的概念,理解函数在一点连续的几何意义,掌握判断简单函数(包括分段函数)在一点的连续性;
( 13 )会求函数的间断点及确定其类型。
( 14 )了解初等函数在其定义域区间的连续性, 了解闭区间上连续函数的性质。
2、一元函数的微分学
( 1)理解导数概念, 导数的经济意义及其几何意义, 知道可导与 连续的关系,能用定义求函数在一点处的导数, 会求曲线上一点处的切线方程与法线方程;
( 2)熟练掌握导数基本公式、四则运算法则及复合函数的求导方 法;
( 3)掌握隐函数求导法, 了解对数求导法,知道反函数求导法;
( 4)理解高阶导数概念,会求高阶导数(以二阶导数为主);
( 5)理解函数的微分概念, 掌握微分法则、可微与可导的关系,
会求函数的一阶微分。
3、中值定理及导数的应用
( 1)知道罗尔定理、拉格朗日中值定理的条件及结论, 会求值;
( 2)熟练掌握并利用洛必达法则求各种未定式极限;
( 3) 掌握用导数判别函数单调性的方法,理解函数极值的概念; ( 4)理解驻点、极值点、最值点的概念, 知道极值点与驻点、不可导点的关系,掌握利用一阶导数求函数极值、最值的方法,并会求 解简单的应用问题(包括经济分析中的问题);
( 5)知道边际及弹性概念, 会求经济函数边际值和边际函数(重 点是边际成本、边际收益、边际利润) 用其经济意义,会求需求函数 的需求弹性;
( 6)会判断曲线的凸性,会求曲线的拐点;
( 7)知道函数图象的描绘。
4、不定积分
( 1)理解并掌握原函数与不定积分的概念及其关系, 掌握不定积分的性质,了解原函数存在定理;
( 2)熟练掌握不定积分的基本积分公式;
( 3) 熟练掌握直接积分法、第一类换元法积分法、第二类换元法 中的幂代换法(被积函数中含有 的因子)、分部积分法。会第二 类换元法中的三角代换法(弦变、切变、割变);
( 4 )会求简单有理函数的不定积分(分解定理可以不作要求),
会求一些简单的无理函数及三角函数有理式的不定积分。
5、定积分
( 1)理解定积分的概念及其几何意义,了解函数可积的条件;
( 2)掌握定积分的基本性质;
( 3) 理解变上限积分函数及其导数;
( 4)熟练掌握定积分的计算方法;
( 5)了解无穷区间上广义积分的概念,掌握其计算方法;
( 6 )掌握用定积分计算平面图形的面积以及解决简单的经济问题。
6、多元函数的微积分学
( 1)了解空间直角坐标系的意义;
(2) 了解二元函数的概念、几何意义, 了解二元函数的极限和连续的概念, 会求二元函数的定义域;
( 3) 理解偏导数概念, 了解全微分概念, 知道全微分存在的必要
条件和充分条件;
( 4)掌握二元函数的一、二阶偏导数的求法, 会求二元函数的全 微分;
( 5)掌握复合函数一阶偏导数的求法,会求隐函数的偏导数;
(6) 会求二元函数的无条件极值, 会利用拉格朗日乘数法求简单 的条件极值。
( 7)了解二重积分的概念及其几何含义, 会计算一些简单的二重积分。
7、无穷级数
( 1)理解无穷级数收敛、发散以及其和的概念, 了解无穷级数的基本性质及收敛的必要条件;
( 2)熟悉几何级数、 p —级数的敛散条件;
( 3) 掌握正项级数的比较判别法与比值判别法, 知道正项级数的 根值判别法, 理解任意项级数绝对收敛的概念, 了解条件收敛的概念, 掌握任意项级数的莱布尼兹判别法;
( 4)理解幂级数的概念,并能熟练地判定其收敛半径和收敛区间,知道和函数及其计算。
8、微分方程初步
( 1)了解微分方程、解、通解、初始条件和特解的概念;
( 2 )熟练掌握可分离变量的微分方程及一阶线性微分方程的解法;
( 3) 会解齐次型方程和贝努利方程, 了解全微分方程的概念及其
解法;

( 5)理解二阶线性微分方程的解的结构, 熟练掌握二阶常系数齐
次线性微分方程的解法;
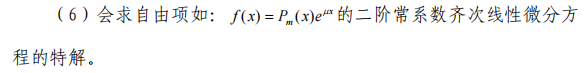
9、矩阵代数
( 1)理解n 阶行列式定义, 掌握行列式的运算性质, 熟练掌握二 阶、三阶和四阶行列式的计算法,掌握计算特殊的n 阶行列式的方法;
知道行列式展开的拉普拉斯(Laplace)定理;
( 2)理解矩阵的概念。了解单位矩阵、对角矩阵、三角矩阵、对 称矩阵和反对称矩阵,以及它们的性质, 熟练掌握矩阵的线性运算(矩 阵的加法与减法, 数乘矩阵), 乘法运算, 矩阵的转置, 知道方阵的幂 及其运算规律;
( 3) 理解逆矩阵的概念以及矩阵可逆的充要条件, 了解伴随矩 阵的概念及性质,掌握用伴随矩阵求逆矩阵的方法;
( 4)理解矩阵的秩的概念, 知道矩阵等价的概念和初等矩阵的性 质,熟练掌握矩阵的初等变换及其用初等变换求矩阵的秩和逆矩阵的
方法;
( 5)理解n 维向量的概念, 知道内积的概念, 会求向量的长度, 理解向量组线性相关、线性无关的定义, 了解并会用向量组线性相关、 线性无关的有关重要结论,掌握判断向量组线性相关性的方法,了解 向量组的秩及极大无关组的概念,熟练掌握求秩及极大无关组的方法 (主要是利用矩阵的初等变换), 了解向量组的秩与矩阵秩的关系;
( 6)了解克莱姆(Cramer)法则, 理解齐次线性方程组有解与无解 的充要条件及非齐次线性方程组有解与无解的充要条件, 理解线性方 程组的基础解系、通解等概念及解的结构,熟练掌握用初等行变换求 解线性方程组的方法;
附件下载:附件4:2023年专升本考试大纲《高等数学》考试大纲(文史类、财经类、管理类、医学类).pdf


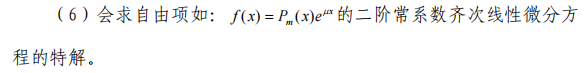





.png)